Subiectul I
1.
5
Rezultatul calculului este egal cu:
Rezultatul calculului
este egal cu:
A
B
C
D
2.
5
Știind că , atunci rezultatul calculului este egal cu:
Știind că
, atunci rezultatul calculului
este egal cu:
A
B
C
D
3.
5
Suma numerelor întregi din intervalul este egală cu:
Suma numerelor întregi din intervalul
este egală cu:
A
B
C
D
4.
5
În tabelul de mai jos este prezentată situația notelor obținute de elevii claselor a VIII-a dintr-o școală, la un test de matematică:
Media notelor obținute de elevii claselor a VIII-a din această școală la testul de matematică este egală cu:
În tabelul de mai jos este prezentată situația notelor obținute de elevii claselor a VIII-a dintr-o școală, la un test de matematică:
Media notelor obținute de elevii claselor a VIII-a din această școală la testul de matematică este egală cu:
A
B
C
D
5.
5
Patru elevi, Ioana, Mara, Petrică și Ștefan, au calculat produsul numerelor și , iar rezultatele obținute sunt prezentate în tabelul de mai jos:
Conform informațiilor din tabel, rezultatul corect a fost obținut de:
Patru elevi, Ioana, Mara, Petrică și Ștefan, au calculat produsul numerelor
și
, iar rezultatele obținute sunt prezentate în tabelul de mai jos:
Conform informațiilor din tabel, rezultatul corect a fost obținut de:
A
Ioana
B
Mara
C
Petrică
D
Ștefan
6.
5
O mașină se deplasează în intervalul orar 12:56 – 14:26 cu o viteză medie de 80 km/h. Mihai afirmă că, în acest interval de timp, mașina a parcurs o distanță egală cu 200 km. Afirmatia lui Mihai este:
O mașină se deplasează în intervalul orar 12:56 – 14:26 cu o viteză medie de 80 km/h. Mihai afirmă că, în acest interval de timp, mașina a parcurs o distanță egală cu 200 km. Afirmatia lui Mihai este:
A
adevărată
B
falsă
Subiectul al II-lea
1.
5
În figura alăturată punctele și sunt coliniare, în această ordine, astfel încât cm și cm. Știind că punctul este mijlocul segmentului , iar punctul este mijlocul segmentului , lungimea segmentului este egală cu:
În figura alăturată punctele
și
sunt coliniare, în această ordine, astfel încât
cm și
cm. Știind că punctul
este mijlocul segmentului
, iar punctul
este mijlocul segmentului
, lungimea segmentului
este egală cu:
A
cm
B
cm
C
cm
D
cm
2.
5
În figura alăturată sunt reprezentate unghiurile opuse la vârf și . Măsura unghiului este egală cu . Măsura unghiului este egală cu: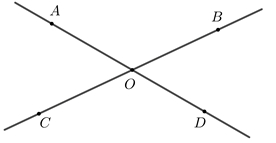
În figura alăturată sunt reprezentate unghiurile opuse la vârf
și
. Măsura unghiului
este egală cu
. Măsura unghiului
este egală cu:
A
B
C
D
3.
5
În figura alăturată este reprezentat triunghiul , dreptunghic în , cu cm și măsura unghiului este egală cu . Lungimea segmentului este egală cu: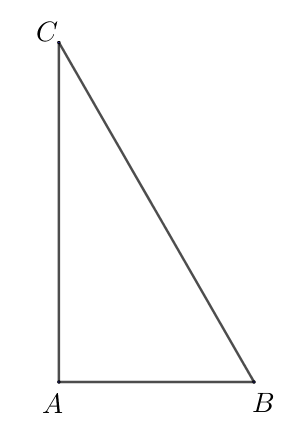
În figura alăturată este reprezentat triunghiul
, dreptunghic în
, cu
cm și măsura unghiului
este egală cu
. Lungimea segmentului
este egală cu:
A
cm
B
cm
C
cm
D
cm
4.
5
În figura alăturată este reprezentat paralelogramul , cu și măsura unghiului este egală cu . Măsura unghiului este egală cu:
În figura alăturată este reprezentat paralelogramul
, cu
și măsura unghiului
este egală cu
. Măsura unghiului
este egală cu:
A
B
C
D
5.
5
În figura alăturată este reprezentat triunghiul , cu cm, înscris într-un cerc care are raza egală cu cm. Măsura unghiului este egală cu: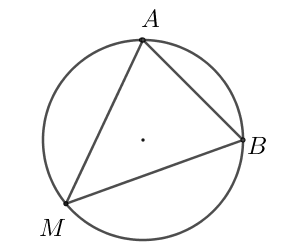
În figura alăturată este reprezentat triunghiul
, cu
cm, înscris într-un cerc care are raza egală cu
cm. Măsura unghiului
este egală cu:
A
B
C
D
6.
5
În figura alăturată este reprezentat un con circular drept care are secțiunea axială un triunghi echilateral cu înălțimea egală cu cm. Generatoarea conului are lungimea egală cu: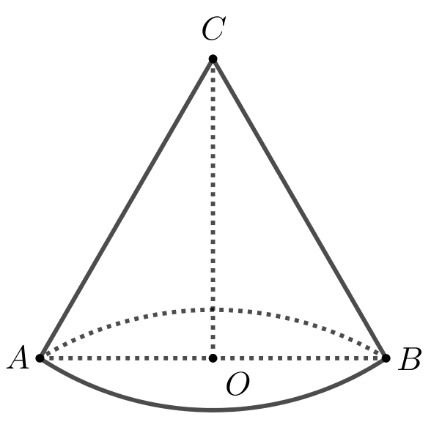
În figura alăturată este reprezentat un con circular drept care are secțiunea axială un triunghi echilateral cu înălțimea egală cu
cm. Generatoarea conului are lungimea egală cu:
A
cm
B
cm
C
cm
D
cm
Subiectul al III-lea
1.
5
Un excursionist a parcurs un traseu în trei zile. În prima zi a parcurs 30% din lungimea traseului, în a doua zi o treime din distanța parcursă în prima zi, iar în a treia zi a parcurs restul de 72 km.
Un excursionist a parcurs un traseu în trei zile. În prima zi a parcurs 30% din lungimea traseului, în a doua zi o treime din distanța parcursă în prima zi, iar în a treia zi a parcurs restul de 72 km.
a.
2
Este posibil ca distanța parcursă de excursionist în a doua zi să reprezinte o pătrime din lungimea întregului traseu? Justifică răspunsul dat.
b.
3
Determină lungimea traseului parcurs de excursionist în cele trei zile.
2.
5
Se consideră expresia , unde .
Se consideră expresia
, unde
.
a.
2
Arată că
, pentru orice
.
b.
3
Determină numerele întregi
pentru care
.
3.
5
Se consideră funcția .
Se consideră funcția
.
a.
2
Rezolvă ecuația
.
b.
3
Știind că
și
sunt punctele de intersecție a reprezentării grafice a funcției
cu axele
respectiv
ale sistemului de axe ortogonale
, iar punctul
este simetricul punctului
față de punctul
, determină coordonatele punctului
.
4.
5
În figura alăturată este reprezentat pătratul cu cm și triunghiul echilateral .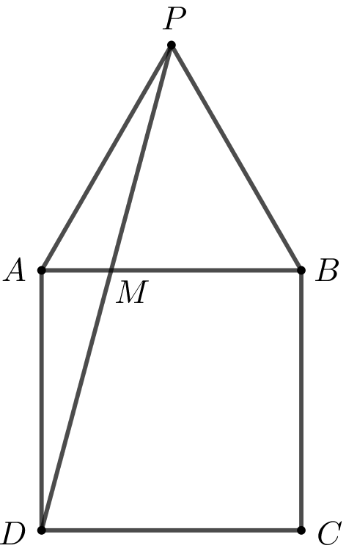
În figura alăturată este reprezentat pătratul
cu
cm și triunghiul echilateral
.
a.
2
Arată că măsura unghiului
este egală cu
.
b.
3
Demonstrează că
cm, unde
.
5.
5
În figura alăturată este reprezentat trapezul cu , cm și cm. Punctele și sunt mijloacele laturilor , , respectiv .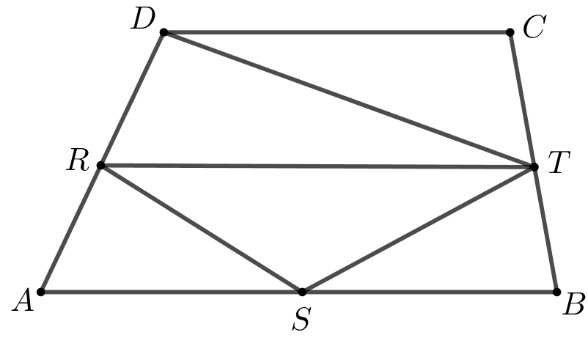
În figura alăturată este reprezentat trapezul
cu
,
cm și
cm. Punctele
și
sunt mijloacele laturilor
,
, respectiv
.
a.
2
Arată că lungimea segmentului
este egală cu
cm.
b.
3
Arată că aria patrulaterului
este egală cu jumătate din aria trapezului
.
6.
5
În figura alăturată este reprezentat cubul cu cm.
În figura alăturată este reprezentat cubul
cu
cm.
a.
2
Arată că volumul cubului
este egal cu
cm³.
b.
3
Demonstrează că dreapta
este perpendiculară pe planul
, unde
și
.
© 2024 ZeceLaEN.ro