Subiectul I
1.
5
Rezultatul calculului este:
Rezultatul calculului
este:
A
B
C
D
2.
5
Numărul întreg care verifică ecuația este:
Numărul întreg
care verifică ecuația
este:
A
B
C
D
3.
5
Suma numerelor naturale prime, mai mici decât , este:
Suma numerelor naturale prime, mai mici decât
, este:
A
B
C
D
4.
5
Ordinea crescătoare a numerelor este:
Ordinea crescătoare a numerelor
este:
A
B
C
D
5.
5
Calculând din se obține:
Calculând
din
se obține:
A
B
C
D
6.
5
Andrei afirmă că valoarea absolută a numărului este . Afirmația lui Andrei este:
Andrei afirmă că valoarea absolută a numărului
este
. Afirmația lui Andrei este:
A
adevărată
B
falsă
Subiectul al II-lea
1.
5
În figura alăturată, punctele sunt coliniare în această ordine, astfel încât . Punctele sunt mijloacele segmentelor , respectiv . Lungimea segmentului este egală cu: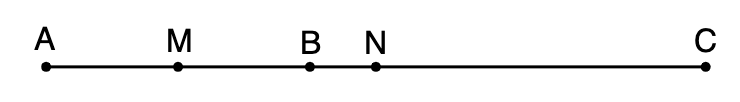
În figura alăturată, punctele
sunt coliniare în această ordine, astfel încât
. Punctele
sunt mijloacele segmentelor
, respectiv
. Lungimea segmentului
este egală cu:
A
B
C
D
2.
5
În figura alăturată, unghiurile sunt congruente, astfel încât punctele sunt coliniare. Măsura unghiului este egală cu: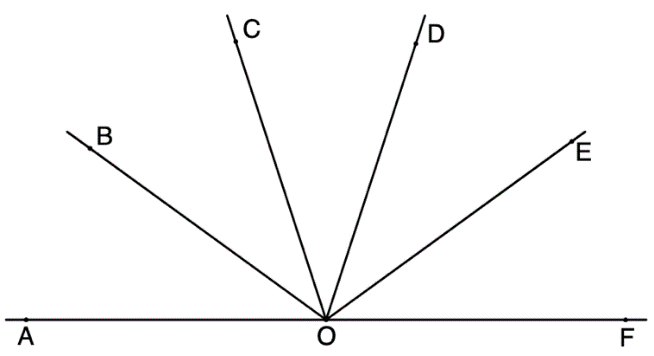
În figura alăturată, unghiurile
sunt congruente, astfel încât punctele
sunt coliniare. Măsura unghiului
este egală cu:
A
B
C
D
3.
5
Punctele sunt mijloacele laturilor triunghiului cu perimetrul egal cu . Perimetrul triunghiului este egal cu: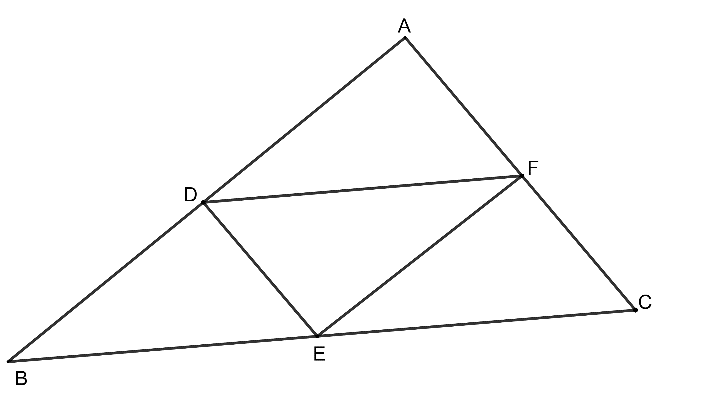
Punctele
sunt mijloacele laturilor triunghiului
cu perimetrul egal cu
. Perimetrul triunghiului
este egal cu:
A
B
C
D
4.
5
Trapezul are baza mare egală cu diagonala și . Măsura unghiului este egală cu:
Trapezul
are baza mare
egală cu diagonala
și
. Măsura unghiului
este egală cu:
A
B
C
D
5.
5
În figura alăturată sunt reprezentate două cercuri concentrice de centru și raze și . Coarda este tangentă în punctul la cercul mai mic. Știind că și , lungimea segmentului este egală cu:
În figura alăturată sunt reprezentate două cercuri concentrice de centru
și raze
și
. Coarda
este tangentă în punctul
la cercul mai mic. Știind că
și
, lungimea segmentului
este egală cu:
A
B
C
D
6.
5
Piramida patrulateră regulată are toate muchiile congruente. Măsura unghiului dintre dreptele și este de: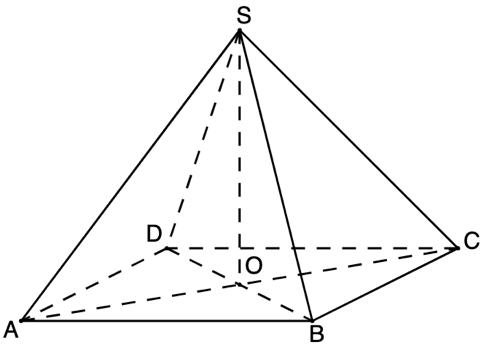
Piramida patrulateră regulată
are toate muchiile congruente. Măsura unghiului dintre dreptele
și
este de:
A
B
C
D
Subiectul al III-lea
1.
5
Media aritmetică a două numere naturale este . Împărțind un număr la celălalt, se obține câtul și restul egal cu .
Media aritmetică a două numere naturale este
. Împărțind un număr la celălalt, se obține câtul
și restul egal cu
.
a.
2
Poate fi numărul mai mare egal cu
? Justificați răspunsul.
b.
3
Aflați cele două numere.
2.
5
Fie numărul .
Fie numărul
.
a.
2
Arătați că
.
b.
3
Dacă
, calculați
.
3.
5
Fie ,
Fie
,
a.
2
Arătați că
.
b.
3
Rezolvați în mulțimea numerelor întregi ecuația
.
4.
5
În exteriorul triunghiului dreptunghic , cu catetele și , se construiesc triunghiurile dreptunghice isoscele și cu ipotenuzele și respectiv .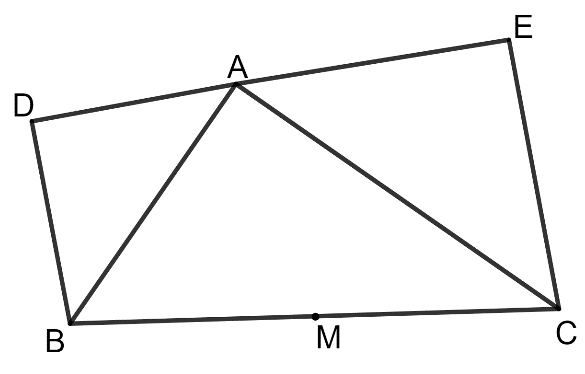
În exteriorul triunghiului dreptunghic
, cu catetele
și
, se construiesc triunghiurile dreptunghice isoscele
și
cu ipotenuzele
și respectiv
.
a.
2
Arătați că punctele
sunt puncte coliniare.
b.
3
Dacă
este mijlocul laturii
,
și
, calculați aria patrulaterului
.
5.
5
În figura alăturată sunt reprezentate două pătrate, și , având laturile de . Punctul este mijlocul lui , iar .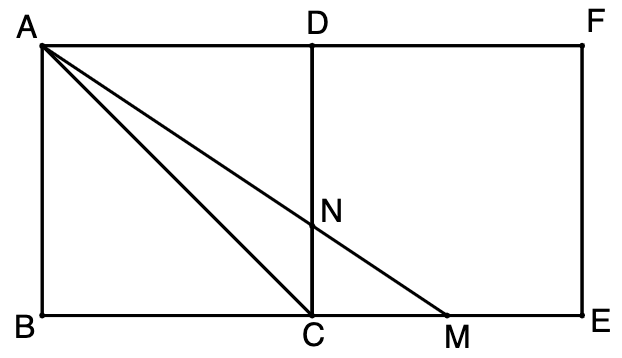
În figura alăturată sunt reprezentate două pătrate,
și
, având laturile de
. Punctul
este mijlocul lui
, iar
.
a.
2
Arătați că
.
b.
3
Calculați sinusul unghiului
.
6.
5
În figura alăturată este reprezentat un paralelipiped dreptunghic cu , și este pătrat.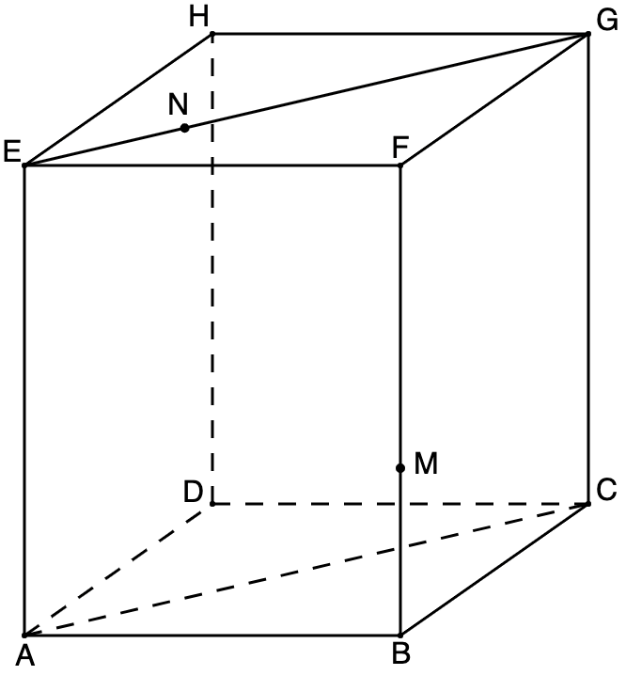
În figura alăturată este reprezentat un paralelipiped dreptunghic
cu
,
și
este pătrat.
a.
2
Arătați că
.
b.
3
Punctele
și
aparțin segmentelor
și respectiv
, astfel încât
. Calculați tangenta unghiului format de dreapta
cu planul
.
© 2024 ZeceLaEN.ro