Subiectul I
1.
5
Rezultatul calculului este egal cu:
Rezultatul calculului
este egal cu:
A
B
C
D
2.
5
Dacă , atunci este egal cu:
Dacă
, atunci
este egal cu:
A
B
C
D
3.
5
Probabilitatea ca, alegând la întâmplare un element al mulțimii , acesta să fie număr prim este egală cu:
Probabilitatea ca, alegând la întâmplare un element al mulțimii
, acesta să fie număr prim este egală cu:
A
B
C
D
4.
5
În tabelul de mai jos este prezentată situația notelor obținute de elevii clasei a VIII-a dintr-o școală, la un test la matematică:
Procentul elevilor care au obținut note mai mari decât 7 din numărul total de elevi este egal cu:
În tabelul de mai jos este prezentată situația notelor obținute de elevii clasei a VIII-a dintr-o școală, la un test la matematică:
Procentul elevilor care au obținut note mai mari decât 7 din numărul total de elevi este egal cu:
A
B
C
D
5.
5
Patru elevi, Maria, Cristina, Ștefan și Mihai, au calculat media geometrică a numerelor și . Rezultatele obținute de elevi sunt prezentate în tabelul de mai jos:
Dintre cei patru elevi, rezultatul corect a fost obținut de:
Patru elevi, Maria, Cristina, Ștefan și Mihai, au calculat media geometrică a numerelor
și
. Rezultatele obținute de elevi sunt prezentate în tabelul de mai jos:
Dintre cei patru elevi, rezultatul corect a fost obținut de:
A
Maria
B
Cristina
C
Ștefan
D
Mihai
6.
5
Afirmatia „Numărul aparține intervalului ” este:
Afirmatia „Numărul
aparține intervalului
” este:
A
adevărată
B
falsă
Subiectul al II-lea
1.
5
În figura alăturată punctele A, C, D și B sunt coliniare, în această ordine, astfel încât , . Dacă cm, atunci lungimea segmentului CD este egală cu:
În figura alăturată punctele A, C, D și B sunt coliniare, în această ordine, astfel încât
,
. Dacă
cm, atunci lungimea segmentului CD este egală cu:
A
cm
B
cm
C
cm
D
cm
2.
5
În figura următoare, dreptele și sunt paralele și sunt intersectate de secanta , fiind evidențiate măsurile a două unghiuri de și respectiv . Valoarea lui este egală cu: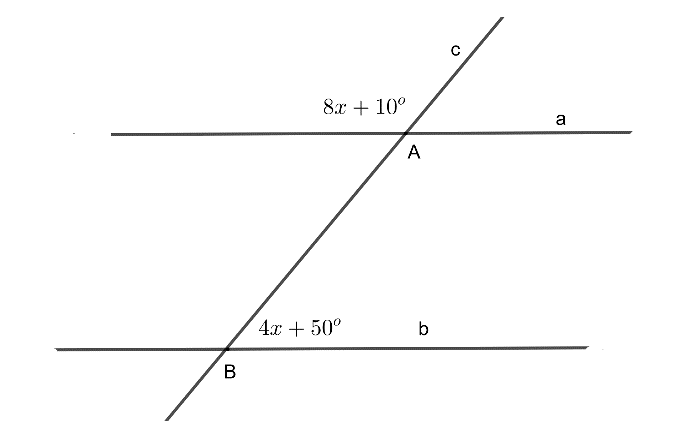
În figura următoare, dreptele
și
sunt paralele și sunt intersectate de secanta
, fiind evidențiate măsurile a două unghiuri de
și respectiv
. Valoarea lui
este egală cu:
A
B
C
D
3.
5
Fie triunghiul dreptunghic în și , . Dacă cm, măsura unghiului este egală cu , iar este bisectoarea unghiului , atunci lungimea segmentului este egală cu: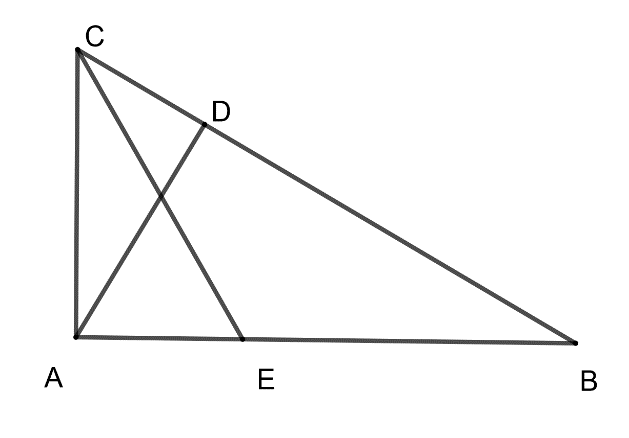
Fie triunghiul
dreptunghic în
și
,
. Dacă
cm, măsura unghiului
este egală cu
, iar
este bisectoarea unghiului
, atunci lungimea segmentului
este egală cu:
A
cm
B
cm
C
cm
D
cm
4.
5
În cercul de centru din figura alăturată măsura unghiului este egală cu , iar este un punct pe acest cerc. Atunci măsura unghiului este egală cu:
În cercul de centru
din figura alăturată măsura unghiului
este egală cu
, iar
este un punct pe acest cerc. Atunci măsura unghiului
este egală cu:
A
B
C
D
5.
5
În figura alăturată este reprezentat trapezul isoscel cu , cm, cm, iar măsura unghiului este egală cu . Aria trapezului este egală cu: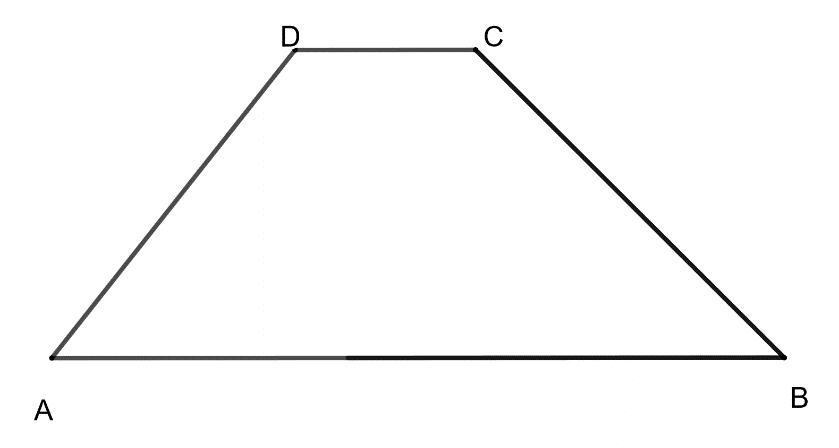
În figura alăturată este reprezentat trapezul isoscel
cu
,
cm,
cm, iar măsura unghiului
este egală cu
. Aria trapezului
este egală cu:
A
cm
B
cm
C
cm
D
cm
6.
5
În figura alăturată este reprezentat cubul . Dacă punctele reprezintă centrele fețelor , , , respectiv , atunci măsura unghiului determinat de dreptele și este egală cu: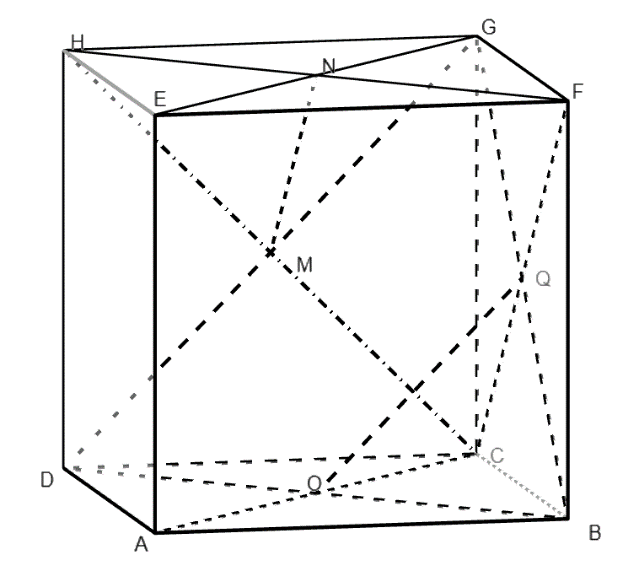
În figura alăturată este reprezentat cubul
. Dacă punctele
reprezintă centrele fețelor
,
,
, respectiv
, atunci măsura unghiului determinat de dreptele
și
este egală cu:
A
B
C
D
Subiectul al III-lea
1.
5
Matei și Vlad sunt frați. Suma vârstelor lor este 21 ani, iar în urmă cu 3 ani, vârsta lui Matei era jumătate din vârsta lui Vlad.
Matei și Vlad sunt frați. Suma vârstelor lor este 21 ani, iar în urmă cu 3 ani, vârsta lui Matei era jumătate din vârsta lui Vlad.
a.
2
Este posibil ca Vlad să aibă în prezent 8 ani? Justifică răspunsul dat.
b.
3
Determină peste câți ani vârsta lui Matei va fi două treimi din vârsta lui Vlad.
2.
5
Se consideră expresia .
Se consideră expresia
.
a.
2
Arată că
, oricare ar fi numărul real
.
b.
3
Arată că
, pentru orice număr real
.
3.
5
Se consideră numerele reale: și .
Se consideră numerele reale:
și
.
a.
2
Arată că
.
b.
3
Arată că dacă
, atunci
este număr natural.
4.
5
În figura alăturată este reprezentat triunghiul echilateral cu cm. Notăm cu mijlocul laturii și construim din perpendiculara pe care intersectează pe în și paralela prin la în .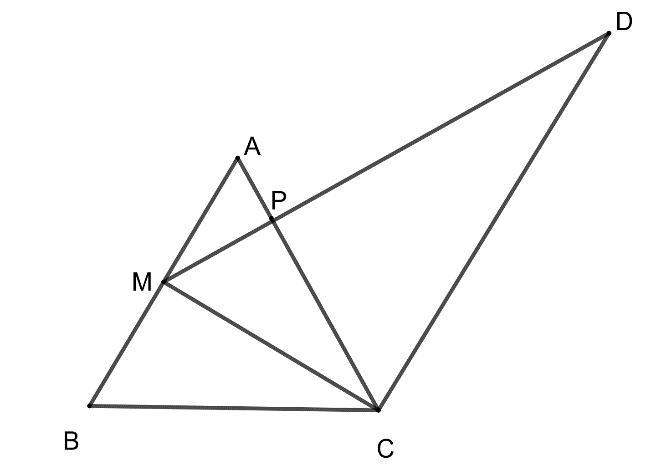
În figura alăturată este reprezentat triunghiul echilateral
cu
cm. Notăm cu
mijlocul laturii
și construim din
perpendiculara pe
care intersectează pe
în
și paralela prin
la
în
.
a.
2
Arată că lungimea segmentului
este egală cu
cm.
b.
3
Arată că aria patrulaterului
este dublul ariei triunghiului
.
5.
5
În figura alăturată este reprezentat trapezul dreptunghic cu , , cm și cm. Punctul aparține segmentului , astfel încât cm și intersecția dreptelor și este punctul .
În figura alăturată este reprezentat trapezul dreptunghic
cu
,
,
cm și
cm. Punctul
aparține segmentului
, astfel încât
cm și intersecția dreptelor
și
este punctul
.
a.
2
Calculează aria trapezului
.
b.
3
Demonstrează că semidreapta
este bisectoarea unghiului
.
6.
5
În figura alăturată este reprezentată piramida patrulateră regulată cu baza pătratul , cm și cm. Punctul este mijlocul segmentului , punctul este mijlocul segmentului și punctul aparține segmentului , astfel încât cm.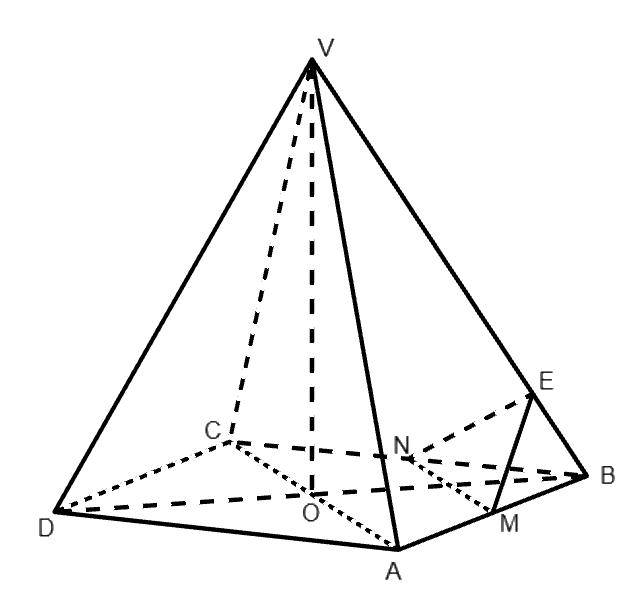
În figura alăturată este reprezentată piramida patrulateră regulată
cu baza pătratul
,
cm și
cm. Punctul
este mijlocul segmentului
, punctul
este mijlocul segmentului
și punctul
aparține segmentului
, astfel încât
cm.
a.
2
Calculează lungimea înălțimii
, unde
.
b.
3
Demonstrează că dreapta
este perpendiculară pe planul
.
© 2024 ZeceLaEN.ro