Subiectul I
1.
5
Rezultatul calculului este:
Rezultatul calculului
este:
A
B
C
D
2.
5
Dacă , atunci rezultatul calculului este:
Dacă
, atunci rezultatul calculului
este:
A
B
C
D
3.
5
Se consideră mulțimile și . Intersecția mulțimilor și este mulțimea:
Se consideră mulțimile
și
. Intersecția mulțimilor
și
este mulțimea:
A
{0, 2, 4, 6, 8}
B
{0, 1, 2, 3, 4, 5, 6, 8}
C
{2, 4, 6}
D
{0, 2, 4, 6}
4.
5
Mulțimea soluțiilor reale ale inecuației este:
Mulțimea soluțiilor reale ale inecuației
este:
A
B
C
D
5.
5
Patru elevi, Ana, Ioan, Dana și Vlad determină numărul . Rezultatele obținute de cei patru elevi sunt prezentate în tabelul de mai jos:
Conform informațiilor din tabel, elevul care a determinat corect numărul este:
Patru elevi, Ana, Ioan, Dana și Vlad determină numărul
. Rezultatele obținute de cei patru elevi sunt prezentate în tabelul de mai jos:
Conform informațiilor din tabel, elevul care a determinat corect numărul
este:
A
Ana
B
Ioan
C
Dana
D
Vlad
6.
5
În diagrama de mai jos sunt prezentate rezultatele obținute de elevii unei clase, la un test de matematică.
Afirmația: „Conform informațiilor din diagramă, jumătate din numărul elevilor acestei clase a obținut la testul de matematică cel puțin nota 8.” este: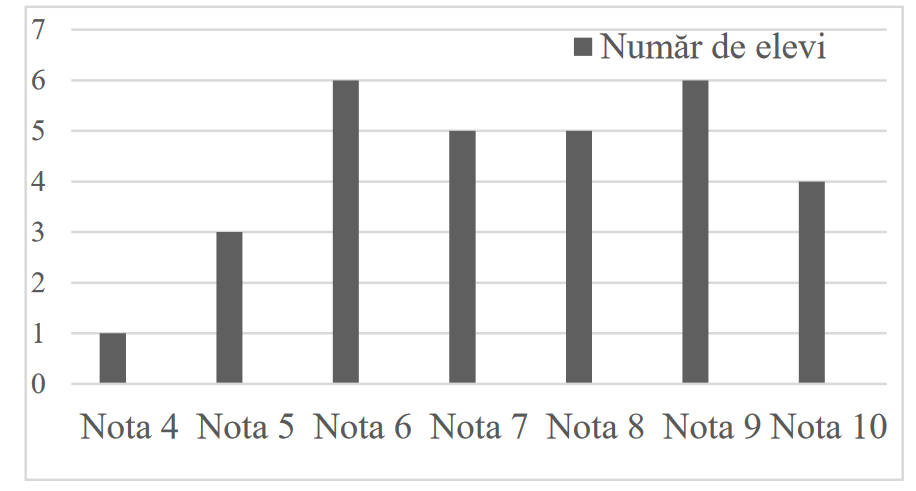
În diagrama de mai jos sunt prezentate rezultatele obținute de elevii unei clase, la un test de matematică.
Afirmația: „Conform informațiilor din diagramă, jumătate din numărul elevilor acestei clase a obținut la testul de matematică cel puțin nota 8.” este:
Afirmația: „Conform informațiilor din diagramă, jumătate din numărul elevilor acestei clase a obținut la testul de matematică cel puțin nota 8.” este:
A
adevărată
B
falsă
Subiectul al II-lea
1.
5
În figura alăturată punctele , , și sunt coliniare, în această ordine, astfel încât , și cm. Punctul este mijlocul segmentului și punctul este mijlocul segmentului . Lungimea segmentului este egală cu:
În figura alăturată punctele
,
,
și
sunt coliniare, în această ordine, astfel încât
,
și
cm. Punctul
este mijlocul segmentului
și punctul
este mijlocul segmentului
. Lungimea segmentului
este egală cu:
A
cm
B
cm
C
cm
D
cm
2.
5
În figura alăturată sunt reprezentate unghiurile adiacente complementare și . Semidreapta este bisectoarea unghiului și . Măsura unghiului este egală cu: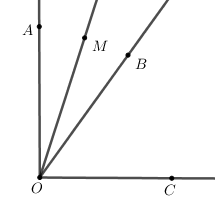
În figura alăturată sunt reprezentate unghiurile adiacente complementare
și
. Semidreapta
este bisectoarea unghiului
și
. Măsura unghiului
este egală cu:
A
B
C
D
3.
5
În figura alăturată este reprezentat triunghiul cu cm și cm. Semidreapta este bisectoarea unghiului și semidreapta este bisectoarea unghiului . Paralela prin punctul la dreapta intersectează dreptele și în punctele , respectiv . Perimetrul triunghiului este egal cu:
În figura alăturată este reprezentat triunghiul
cu
cm și
cm. Semidreapta
este bisectoarea unghiului
și semidreapta
este bisectoarea unghiului
. Paralela prin punctul
la dreapta
intersectează dreptele
și
în punctele
, respectiv
. Perimetrul triunghiului
este egal cu:
A
cm
B
cm
C
cm
D
cm
4.
5
În figura alăturată este reprezentat dreptunghiul , cu cm și triunghiul dreptunghic în . Punctul este mijlocul segmentului și cm. Aria trapezului este egală cu: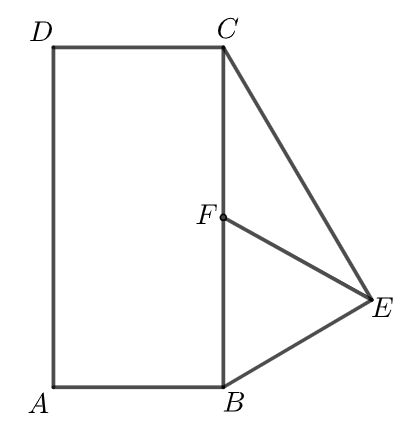
În figura alăturată este reprezentat dreptunghiul
, cu
cm și triunghiul
dreptunghic în
. Punctul
este mijlocul segmentului
și
cm. Aria trapezului
este egală cu:
A
cm
B
cm
C
cm
D
cm
5.
5
În figura alăturată este reprezentat cercul cu centrul în punctul și raza egală cu cm. Punctul este situat la o distanță de cm de centrul cercului. Dreptele și sunt tangente la cerc în punctele și . Măsura arcului mic este egală cu: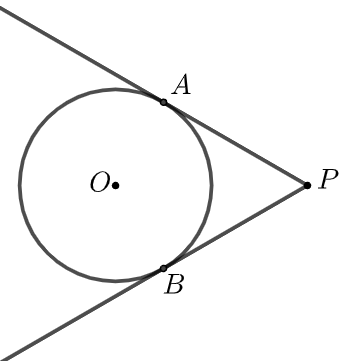
În figura alăturată este reprezentat cercul cu centrul în punctul
și raza egală cu
cm. Punctul
este situat la o distanță de
cm de centrul cercului. Dreptele
și
sunt tangente la cerc în punctele
și
. Măsura arcului mic
este egală cu:
A
B
C
D
6.
5
În figura alăturată este reprezentată piramida patrulateră regulată cu baza , și este punctul de intersecție a dreptelor și . Dacă punctul este mijlocul segmentului , atunci măsura unghiului dreptelor și este egală cu: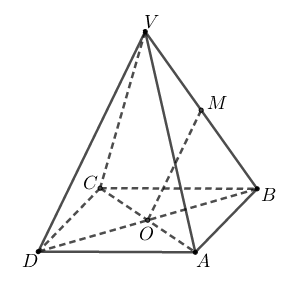
În figura alăturată este reprezentată piramida patrulateră regulată
cu baza
,
și
este punctul de intersecție a dreptelor
și
. Dacă punctul
este mijlocul segmentului
, atunci măsura unghiului dreptelor
și
este egală cu:
A
B
C
D
Subiectul al III-lea
1.
5
Maria aranjează cărțile din bibliotecă și observă că dacă le grupează câte 8, câte 12 sau câte 18 îi rămân de fiecare dată 5 cărți.
Maria aranjează cărțile din bibliotecă și observă că dacă le grupează câte 8, câte 12 sau câte 18 îi rămân de fiecare dată 5 cărți.
a.
2
Verifică dacă Maria poate avea în bibliotecă 53 de cărți. Justifică răspunsul dat.
b.
3
Determină numărul cărților din biblioteca Mariei, știind că acesta este cel mai mic număr natural de trei cifre cu proprietățile din enunț.
2.
5
Se consideră expresia , unde este număr real.
Se consideră expresia
, unde
este număr real.
a.
2
Arată că
.
b.
3
Arată că numărul
este divizibil cu 10, pentru orice număr natural
.
3.
5
Se consideră numărul natural cu cifre nenule, unde și .
Se consideră numărul natural
cu
cifre nenule, unde
și
.
a.
2
Arată că
.
b.
3
Determină numărul
, știind că numerele
și
sunt direct proporționale cu numerele 4 și 3.
4.
5
În figura alăturată este reprezentat triunghiul dreptunghic , cu și . Semidreapta este bisectoarea unghiului , punctul aparține segmentului . Perpendiculara din punctul pe intersectează dreapta în punctul , iar perpendiculara din punctul pe intersectează dreapta în punctul . Dreptele și se intersectează în punctul .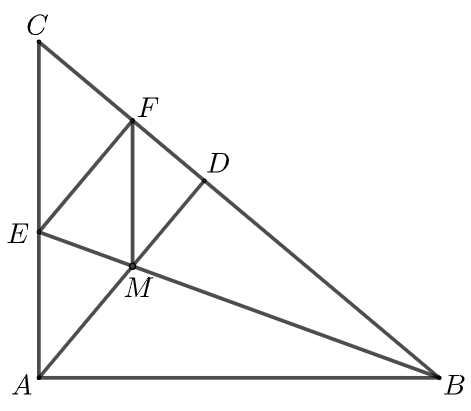
În figura alăturată este reprezentat triunghiul dreptunghic
, cu
și
. Semidreapta
este bisectoarea unghiului
, punctul
aparține segmentului
. Perpendiculara din punctul
pe
intersectează dreapta
în punctul
, iar perpendiculara din punctul
pe
intersectează dreapta
în punctul
. Dreptele
și
se intersectează în punctul
.
a.
2
Arată că măsura unghiului
este egală cu
.
b.
3
Arată că patrulaterul
este romb.
5.
5
În figura alăturată este reprezentat paralelogramul cu cm. Punctul aparține laturii , astfel încât și este punctul de intersecție a dreptelor și .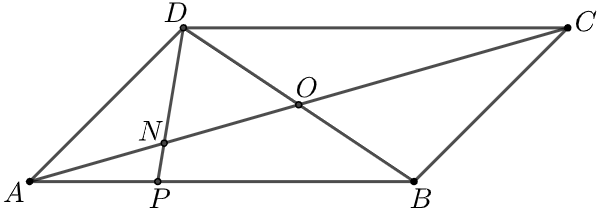
În figura alăturată este reprezentat paralelogramul
cu
cm. Punctul
aparține laturii
, astfel încât
și
este punctul de intersecție a dreptelor
și
.
a.
2
Arată că lungimea segmentului
este egală cu 5 cm.
b.
3
Determină raportul dintre aria triunghiului
și aria triunghiului
, unde
este punctul de intersecție a dreptelor
și
.
6.
5
În figura alăturată este reprezentat cubul . Punctele , , și sunt mijloacele segmentelor , , , respectiv .
În figura alăturată este reprezentat cubul
. Punctele
,
,
și
sunt mijloacele segmentelor
,
,
, respectiv
.
a.
2
Arată că
.
b.
3
Știind că punctul
este mijlocul segmentului
, demonstrează că dreapta
este paralelă cu planul
.
© 2024 ZeceLaEN.ro