Subiectul I
1.
5
Numărul 242 este multiplu al numărului:
Numărul 242 este multiplu al numărului:
A
B
C
D
2.
5
Valoarea lui care verifică egalitatea este egală cu:
Valoarea lui
care verifică egalitatea
este egală cu:
A
B
C
D
3.
5
Opusul numărului este:
Opusul numărului
este:
A
B
C
D
4.
5
Cel mai mare dintre numerele raționale ; ; ; este:
Cel mai mare dintre numerele raționale
;
;
;
este:
A
B
C
D
5.
5
Dacă și , atunci este egal cu:
Dacă
și
, atunci
este egal cu:
A
B
C
D
6.
5
În tabelul următor sunt înregistrate temperaturile medii zilnice dintr-o săptămână.
Dacă temperatura medie din aceea săptămână a fost , atunci este egal cu:
În tabelul următor sunt înregistrate temperaturile medii zilnice dintr-o săptămână.
Dacă temperatura medie din aceea săptămână a fost
, atunci
este egal cu:
A
B
C
D
Subiectul al II-lea
1.
5
În figura alăturată, punctul este mijlocul segmentului , este mijlocul segmentului , iar este simetricul punctului față de punctul B. Valoarea raportului este:
În figura alăturată, punctul
este mijlocul segmentului
,
este mijlocul segmentului
, iar
este simetricul punctului
față de punctul B. Valoarea raportului
este:
A
B
C
D
2.
5
În figura alăturată, unghiurile și sunt adiacente suplementare. Măsura unghiului format de bisectoarele unghiurilor și este: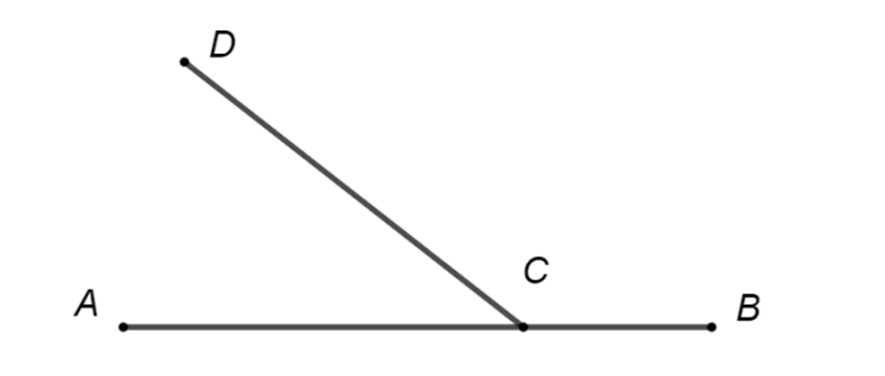
În figura alăturată, unghiurile
și
sunt adiacente suplementare. Măsura unghiului format de bisectoarele unghiurilor
și
este:
A
B
C
D
3.
5
Figura alăturată reprezintă schița unui teren în formă de trapez cu aria de m și lungimea liniei mijlocii de m. Distanța dintre laturile și este egală cu: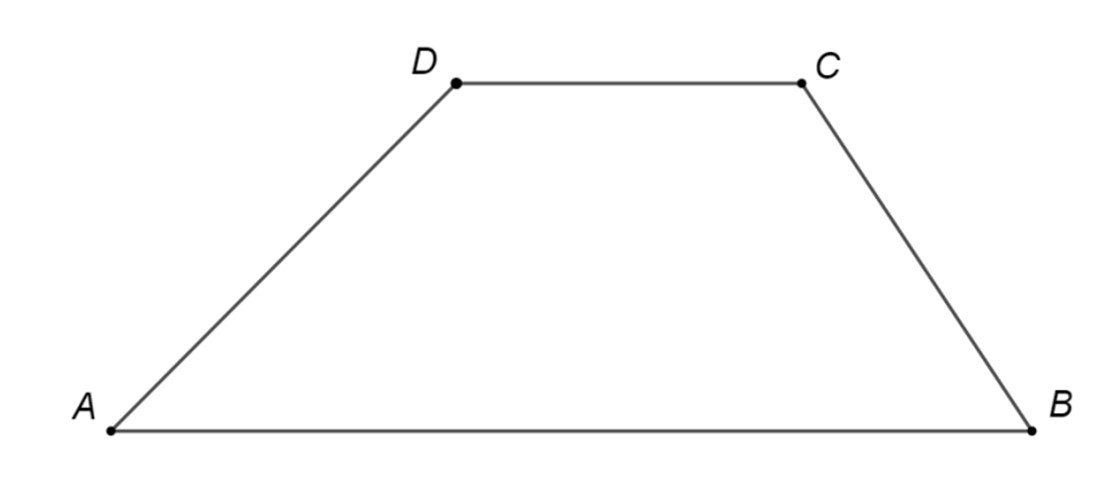
Figura alăturată reprezintă schița unui teren în formă de trapez
cu aria de
m
și lungimea liniei mijlocii de
m. Distanța dintre laturile
și
este egală cu:
A
m
B
m
C
m
D
m
4.
5
Dreptunghiul din figura alăturată are lungimea cm și lățimea cm. Dacă , măsura unghiului este: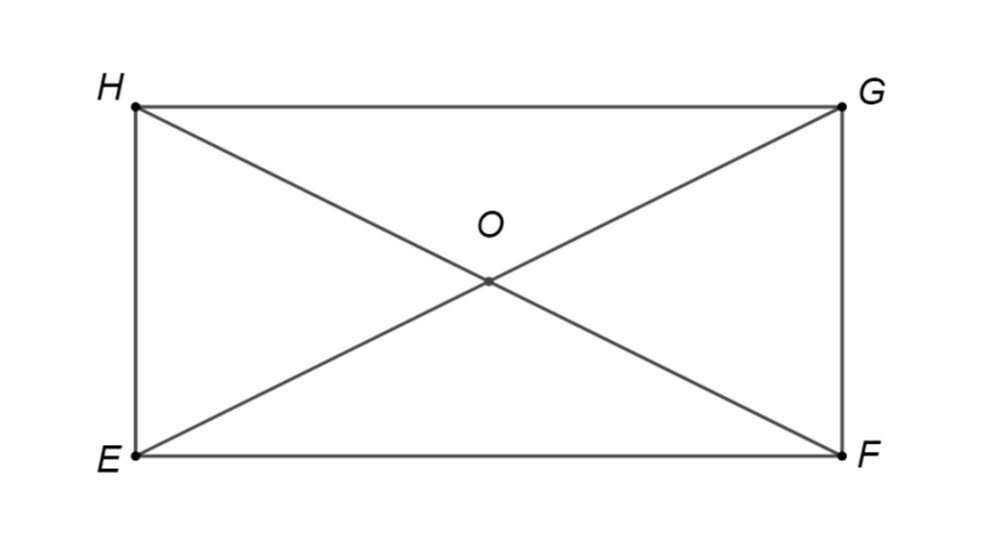
Dreptunghiul
din figura alăturată are lungimea
cm și lățimea
cm. Dacă
, măsura unghiului
este:
A
B
C
D
5.
5
În figura alăturată este un triunghi dreptunghic în cu măsura unghiului de . Dacă lungimea bisectoarei este egală cu cm, atunci lungimea catetei este egală cu: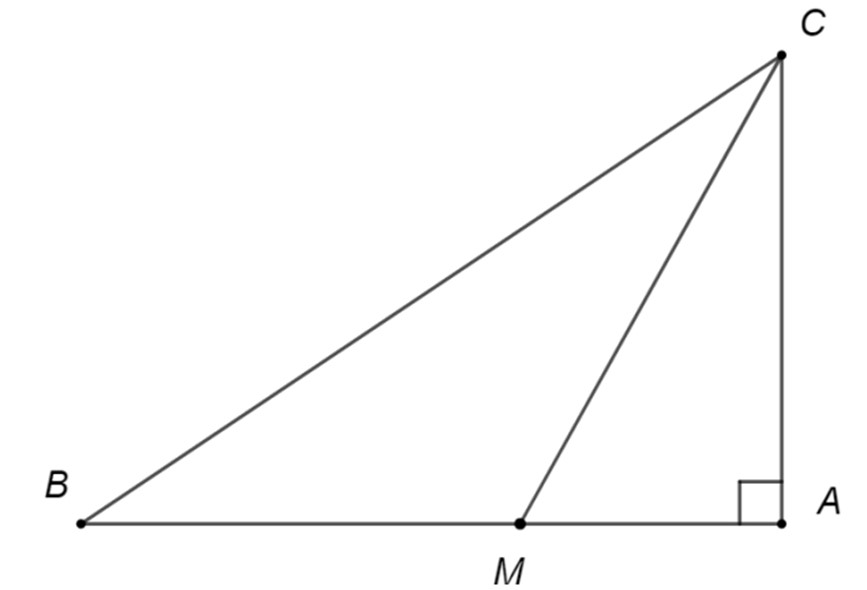
În figura alăturată
este un triunghi dreptunghic în
cu măsura unghiului
de
. Dacă lungimea bisectoarei
este egală cu
cm, atunci lungimea catetei
este egală cu:
A
cm
B
cm
C
cm
D
cm
6.
5
În figura alăturată este un tetraedru regulat cu aria feței egală cu dm. Suma lungimilor tuturor muchiilor tetraedrului este egală cu: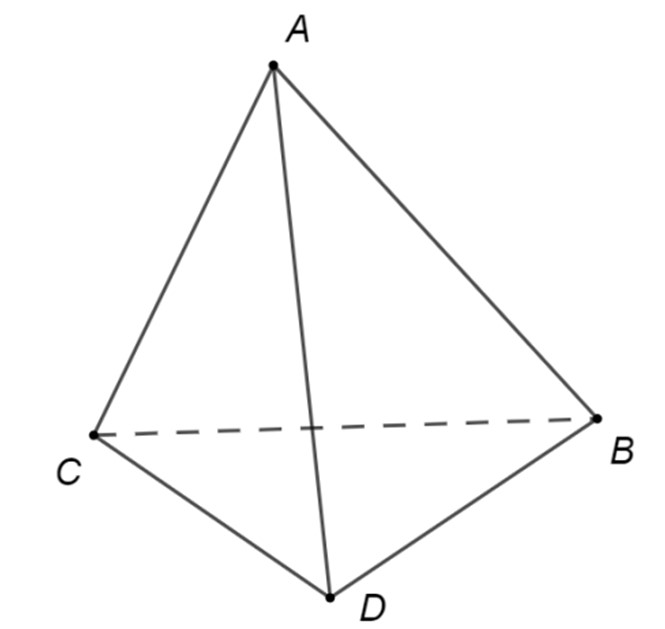
În figura alăturată
este un tetraedru regulat cu aria feței
egală cu
dm
. Suma lungimilor tuturor muchiilor tetraedrului este egală cu:
A
dm
B
dm
C
dm
D
dm
Subiectul al III-lea
1.
5
Radu și Tudor au împreună 800 de lei. Dacă Radu i-ar da lui Tudor o cincime din suma pe care o are, atunci cei doi copii ar avea sume egale.
Radu și Tudor au împreună 800 de lei. Dacă Radu i-ar da lui Tudor o cincime din suma pe care o are, atunci cei doi copii ar avea sume egale.
a.
2
Este posibil ca Radu să aibă 600 de lei? Justifică răspunsul dat.
b.
3
Află ce sumă are Tudor.
2.
5
Se consideră numerele și .
Se consideră numerele
și
.
a.
2
Arată că numărul
.
b.
3
Demonstrează că media geometrică a numerelor
și
este pătrat perfect.
3.
5
Se consideră expresia , unde .
Se consideră expresia
, unde
.
a.
2
Arată că
, pentru orice număr real
.
b.
3
Determină valorile întregi ale lui
pentru care
.
4.
5
Rombul din figura alăturată are înălțimea cm. Se știe că și proiecția a segmentului pe dreapta are lungimea de cm.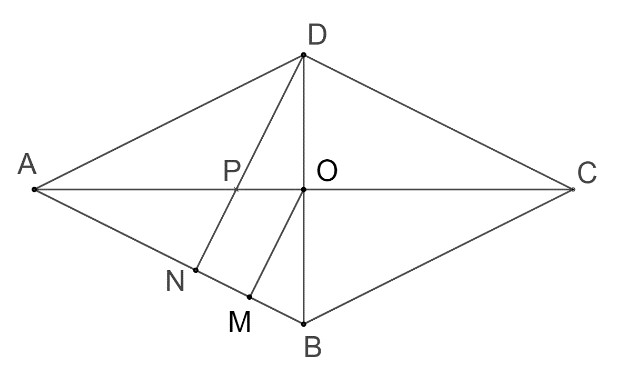
Rombul
din figura alăturată are înălțimea
cm. Se știe că
și proiecția
a segmentului
pe dreapta
are lungimea de
cm.
a.
2
Arată că
cm.
b.
3
Dacă
, calculează aria patrulaterului
.
5.
5
În figura alăturată sunt reprezentate triunghiurile și dreptunghice în , respectiv în . Se știe că , , și .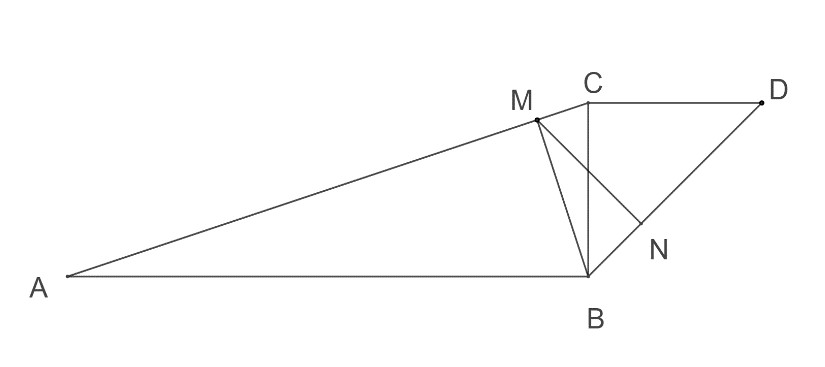
În figura alăturată sunt reprezentate triunghiurile
și
dreptunghice în
, respectiv în
. Se știe că
,
,
și
.
a.
2
Arată că măsura unghiului
este de
.
b.
3
Dacă
cm, află distanța de la
la dreapta
.
6.
5
În figura alăturată este desenată o prismă triunghiulară regulată cu m și m. Punctele , și sunt mijloacele segmentelor , , respectiv .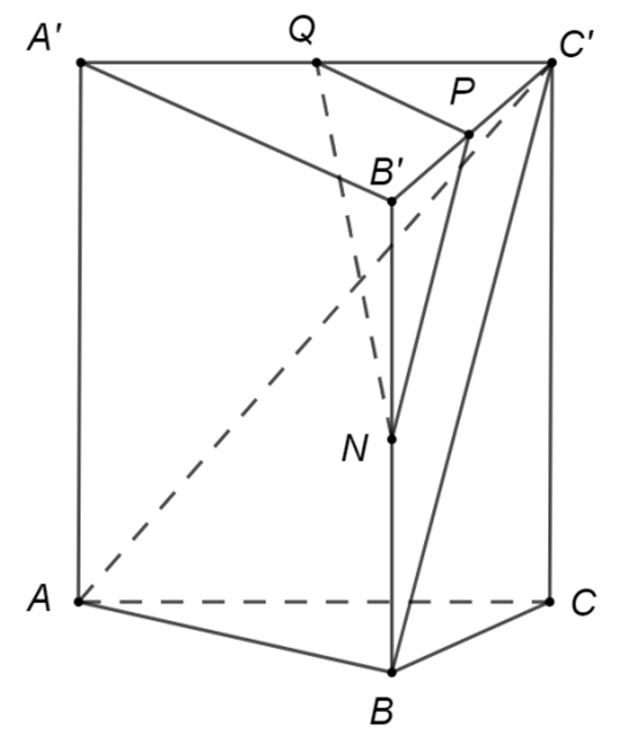
În figura alăturată este desenată o prismă triunghiulară regulată
cu
m și
m. Punctele
,
și
sunt mijloacele segmentelor
,
, respectiv
.
a.
2
Arată că planele
și
sunt paralele.
b.
3
Calculează cosinusul unghiului determinat de dreptele
și
.
© 2024 ZeceLaEN.ro