Subiectul I
1.
5
Rezultatul calculului este egal cu:
Rezultatul calculului
este egal cu:
A
B
C
D
2.
5
Dacă , atunci este egal cu:
Dacă
, atunci
este egal cu:
A
B
C
D
3.
5
Soluția ecuației este numărul:
Soluția ecuației
este numărul:
A
B
C
D
4.
5
Cel mai mic element al mulțimii este:
Cel mai mic element al mulțimii
este:
A
B
C
D
5.
5
Patru elevi, Andra, Marius, Ioana și David, au calculat produsul numerelor și . Rezultatele obținute sunt prezentate în tabelul de mai jos:
Rezultatul corect a fost obținut de către:
Patru elevi, Andra, Marius, Ioana și David, au calculat produsul numerelor
și
. Rezultatele obținute sunt prezentate în tabelul de mai jos:
Rezultatul corect a fost obținut de către:
A
Andra
B
Marius
C
Ioana
D
David
6.
5
Alina afirmă că: „În intervalul de numere reale sunt 7 numere întregi.” Afirmația Alinei este:
Alina afirmă că: „În intervalul de numere reale
sunt 7 numere întregi.” Afirmația Alinei este:
A
adevărată
B
falsă
Subiectul al II-lea
1.
5
În figura alăturată sunt reprezentate punctele coliniare și , în această ordine, astfel încât , iar lungimea segmentului este egală cu 10cm. Lungimea segmentului este egală cu:
În figura alăturată sunt reprezentate punctele coliniare
și
, în această ordine, astfel încât
, iar lungimea segmentului
este egală cu 10cm. Lungimea segmentului
este egală cu:
A
30cm
B
20cm
C
15cm
D
10cm
2.
5
În figura alăturată sunt reprezentate unghiurile opuse la vârf și , cu punctele și coliniare. Măsura unghiului este egală cu și este bisectoarea unghiului . Măsura unghiului este egală cu: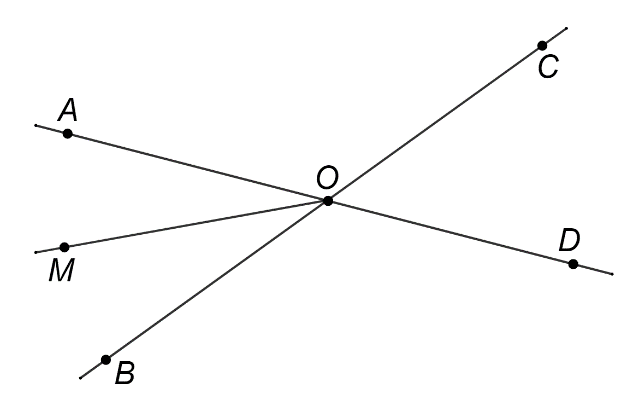
În figura alăturată sunt reprezentate unghiurile opuse la vârf
și
, cu punctele
și
coliniare. Măsura unghiului
este egală cu
și
este bisectoarea unghiului
. Măsura unghiului
este egală cu:
A
B
C
D
3.
5
În figura alăturată este reprezentat triunghiul isoscel cu și . Punctul aparține segmentului , astfel încât . Măsura unghiului este egală cu: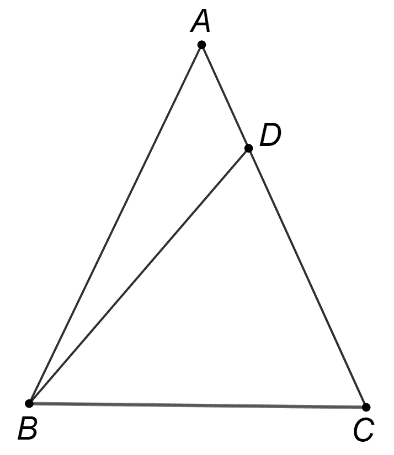
În figura alăturată este reprezentat triunghiul isoscel
cu
și
. Punctul
aparține segmentului
, astfel încât
. Măsura unghiului
este egală cu:
A
B
C
D
4.
5
În figura alăturată este reprezentat paralelogramul cu cm și cm. Perimetrul paralelogramului este egal cu: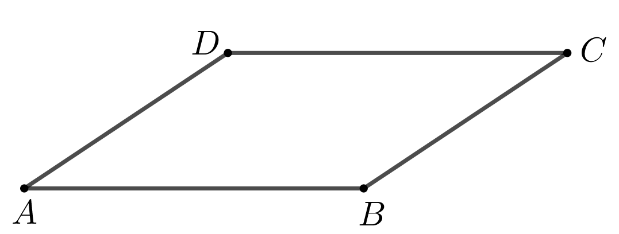
În figura alăturată este reprezentat paralelogramul
cu
cm și
cm. Perimetrul paralelogramului
este egal cu:
A
cm
B
cm
C
cm
D
cm
5.
5
În figura alăturată este reprezentat cercul de centru . Punctele și aparțin cercului, astfel încât măsura unghiului este de și cm. Lungimea cercului este egală cu:
În figura alăturată este reprezentat cercul de centru
. Punctele
și
aparțin cercului, astfel încât măsura unghiului
este de
și
cm. Lungimea cercului este egală cu:
A
10
cm
B
20
cm
C
100
cm
D
200
cm
6.
5
În figura alăturată este reprezentat un con circular drept cu secțiunea axială triunghiul dreptunghic . Înălțimea conului are lungimea egală cu cm. Aria bazei conului este egală cu: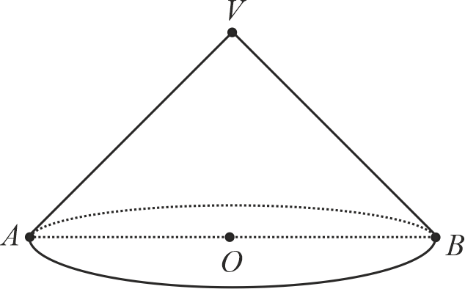
În figura alăturată este reprezentat un con circular drept cu secțiunea axială triunghiul dreptunghic
. Înălțimea conului are lungimea egală cu
cm. Aria bazei conului este egală cu:
A
8 cm
B
16 cm
C
8
cm
D
16
cm
Subiectul al III-lea
1.
5
Mihai a cheltuit o sumă de bani în patru zile. În prima zi a cheltuit 20% din întreaga sumă, în a doua zi 30% din suma rămasă, în a treia zi cu 20 de lei mai mult decât a doua zi, iar în a patra zi a cheltuit ultimii 44 de lei.
Mihai a cheltuit o sumă de bani în patru zile. În prima zi a cheltuit 20% din întreaga sumă, în a doua zi 30% din suma rămasă, în a treia zi cu 20 de lei mai mult decât a doua zi, iar în a patra zi a cheltuit ultimii 44 de lei.
a.
2
Verifică dacă Mihai a cheltuit în a doua zi un sfert din întreaga sumă de bani. Justifică răspunsul dat.
b.
3
Determină suma de bani cheltuită de Mihai, în total, în cele patru zile.
2.
5
Se consideră expresia , unde este un număr real, , și .
Se consideră expresia
, unde
este un număr real,
,
și
.
a.
2
Arată că
, pentru orice număr real
,
și
.
b.
3
Determină numărul natural
pentru care
este număr natural.
3.
5
Se consideră funcția , .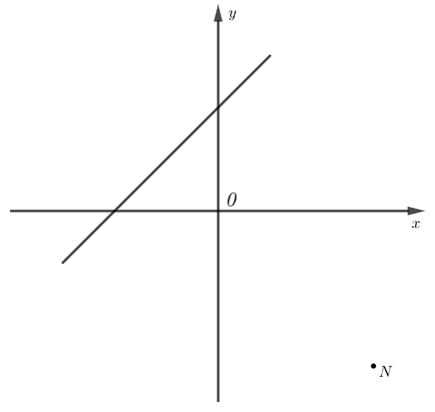
Se consideră funcția
,
.
a.
2
Arată că
.
b.
3
Punctele
și
sunt punctele de intersecție a reprezentării geometrice a graficului funcției
cu axele
, respectiv
, ale sistemului de axe ortogonale
, iar punctul
este mijlocul segmentului
. Arată că punctele
,
și
sunt coliniare, unde
.
4.
5
În figura alăturată este reprezentat dreptunghiul cu cm și cm. Punctul aparține segmentului , astfel încât cm. Prin se duc dreptele și paralele cu dreptele , respectiv . Punctele și aparțin segmentelor și respectiv .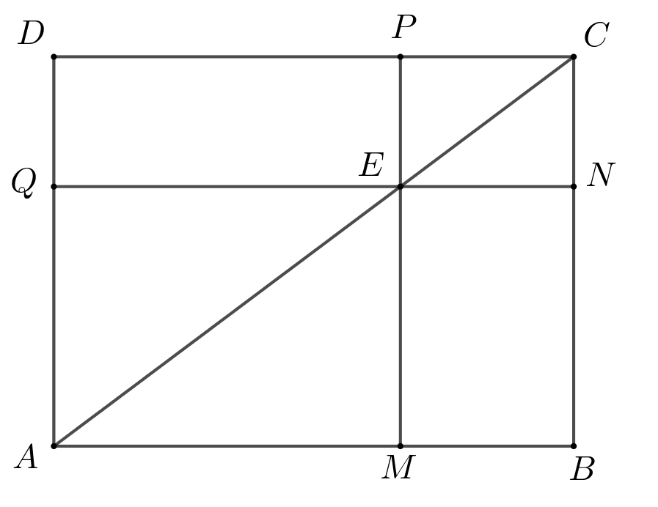
În figura alăturată este reprezentat dreptunghiul
cu
cm și
cm. Punctul
aparține segmentului
, astfel încât
cm. Prin
se duc dreptele
și
paralele cu dreptele
, respectiv
. Punctele
și
aparțin segmentelor
și respectiv
.
a.
2
Arată că
cm.
b.
3
Arată că aria patrulaterului
este de patru ori mai mare decât aria patrulaterului
.
5.
5
În figura alăturată este reprezentat triunghiul , dreptunghic în , cu cm, cm și triunghiul dreptunghic isoscel cu . Punctele și sunt de aceeași parte a dreptei .
În figura alăturată este reprezentat triunghiul
, dreptunghic în
, cu
cm,
cm și triunghiul dreptunghic isoscel
cu
. Punctele
și
sunt de aceeași parte a dreptei
.
a.
2
Arată că perimetrul triunghiului
este egal cu
cm .
b.
3
Calculează distanța de la punctul
la dreapta
.
6.
5
În figura alăturată este reprezentat paralelipipedul dreptunghic cu cm și cm.
În figura alăturată este reprezentat paralelipipedul dreptunghic
cu
cm și
cm.
a.
2
Arată că aria totală a paralelipipedului dreptunghic
este egală cu
cm
.
b.
3
Arată că dreapta
este paralelă cu planul
, unde punctul
este proiecția punctului
pe dreapta
și punctul
este proiecția punctului
pe dreapta
.
© 2024 ZeceLaEN.ro